Universal Gravitation

Orbital Period Calculations

tcrass 0 Comments

*This post re-published & paraphrased from cache – September 30th 2009*

Since this is something that I recently had to do for a game that I’m a developer on, I thought it would be prudent to put together a write-up on the process of determining orbital period of a body around a central mass; specifically sidereal period.  Overall, this is a fairly simple and straight forward problem, but, even so, it is certainly one that every Physics and Astronomy major and enthusiast should be familiar with.

Now, it should be noted that if an object of significant mass is orbiting a central mass, it is probably a good idea to include both masses in the calculation since it could change the result somewhat significantly.  In order to perform this calculation we need to know the following:

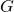  • G, the gravitational constant
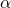  • \alpha, semi-major axis (orbital radius or distance from object 1’s center to object 2’s center)
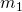  • m_1, the mass of the central object
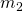  • m_2, the mass of the orbiting object

So, with this information we can derive a formula from Kepler’s Third Law of motion; the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of it’s orbit.

\frac{\alpha^3}{P^3}

and Newton’s Law of Universal Gravitation; attractions are inversely proportional to the squares of the distances between massive bodies.

F=G\frac{(m_1)(m_2)}{r^2}

Now, the formulas need to be combined to achieve the following relationship:

\frac{r^3}{P^2} = \frac{Gm}{4pi^2}

The resultant formula can now be manipulated into solving for P or the period of the orbit as follows:

\frac{1}{P^2} = \frac{Gm}{r^34pi^2} \equiv \frac{r^34pi^2}{Gm} = P^2 \equiv pi\sqrt{\frac{r^3}{Gm}} = P

Important Note: Since we are using the total mass of the combined bodies we do not multiply the masses for this equation, if calculating the period for 2 large bodies the masses should be added together.

Now that we have our formula, it’s time to work through our information.  The central star is a Type A IV star at ~10,000K with a mass of 5.9673*10^30kg.  The planet has a mass of 7.1683*10^24kg and an orbital radius of 5.2360*10^8km.  Next we take this information, along with the Gravitational Constant (6.6730*10^-11m^3kg^-1s^-2 and work through our formula:

2pi\sqrt{\frac{(5.2360*10^8km)^3}{(6.6730*10^-11m^3kg^-1s^-2)((5.9673*10^30kg)+(7.1683*10^24kg))}} = P

Now combine values and convert the orbital radius into meters so our units match:

2pi\sqrt{\frac{(5.2360*10^11m)^3}{3.9820*10^20m^3s^-2}} = P

2pi\sqrt{\frac{1.4355*10^35m^3}{3.9820*10^20m^3s^-2}} = P

Now solve the rest:

2pi\sqrt{3.6060*10^14s^-2} = P \equiv 2pi(1.899*10^7s) = P \equiv 1.1930*10^8s = P

Great! Now we have our answer in seconds which means we can convert this number into years to obtain the yearly orbital comparison (the typical way to express orbital periods when it comes to astronomy).  To do this we take our value, divide by 60 for the 60 seconds in a minute, by 60 again for minutes in an hour, by 24 for the hours in a day and then 365 for the days in a year.

[/math]1.1930*10^8s/60s/60m/24h/365d = 3.7830 years[/math]

And there you have it, our answer for the orbital period of the planet is 3.7830 times longer than that of Earths, or 3.7830 years.

In working through this I think there are a few common problems that can happen, so if you attempt this calculation and do not arrive at an answer you would expect, make sure to check the following things:

  • Make sure orbital period gets converted into meters at some point.  The Gravitational Constant is calculated in meters which means your orbital radius value should be as well.
  • Make sure to add the masses of the bodies.  This is important to note because other similar formulas (such as in calculating weight on another planet) masses are multiplied.  This calculation uses total combined mass.
  • Check your units.  If your calculations are complete but you did not net up with seconds for a unit your calculations could be flawed.

In closing, please let me know if you find any flaws with this write-up.  I have put it together carefully, however, I am not immune to mistakes and have corrected several so far.

How to Calculate Weight on Another Planet

tcrass 3 Comments

*This post re-published from cache – August 28th 2009*

In working on answering a question today, I was rather perturbed by the fact that I was not able to find a definitive answer to a question that I felt should be well defined.  That question was: If I weigh 100lbs on Earth, how much would I weigh on Saturn?

Simple question right?  Not by what I found online.  There are a number of different sites that can be used to get a quick ( and possibly incorrect) answer.  I found the sites that I visited in search of an answer to be at the least, inaccurate and at the most, dead wrong.  The answers ranged from around 55lbs to about 115lbs.  On top of this, the method for calculating weight on another planet was based on the gravitational acceleration at the surface.  This is something that is defined already depending on the site or information you look at, but again, the values varied significantly.

Here’s an easy way to do it and get a reliable answer:

Find the gravitational acceleration, or more specifically the ratio of acceleration in relation to Earth, where Earth is a value of 1.  Now, find a table online with the planet’s ratio that you want to calculate.  For Saturn I used 1.065 (1.07 significant digits) found here.  Simply cross-multiply to get your answer:

\frac{100 lbs.}{1} = \frac{x}{1.07}

100 * 1.07 = x * 1

x = 107 lbs

Now that we have the easy answer I think it is important to understand that without already having the gravitational ratio this is still calculable by obtaining the gravitational ratio on our own, as shown below.

Before we begin, it should be noted that the radius of a planet type body varies from point-to-point.  This means that your answer will also vary depending on where you measure from.  This could account for some of the discrepancies that I found on other sites.  For example, you will be heavier at either of the poles and lighter at the equator.  This is due to the bulge at the equator caused by rotation.  This increases distance from the center of mass and reduces the gravitational forces on you slightly, causing you to weigh less.  For our purposes, we will use the mean radius vs. a specific measurement.

First, we need my mass in kilograms (kg), rather than weight in pounds (lbs) so we use the formula here:  \frac{x}{2.2} = x kg

\frac{100}{2.2} = 45.5 kg

Great, now that we have the mass, we can move forward.  We will need additional information at this point.  The formula that will allow us to make further calculations, Newton’s Law of Universal Gravitation.

F=G\frac{(m_1)(m_2)}{r^2}

It should be noted that the value for r should be in meters, the values of m_1 and m_2 in kilograms and the resultant value of F will be in Newtons.

This formula will allow us to calculate the force exerted between objects of a given mass, at a given distance from the center of gravity.  In turn, allowing us to calculate the respective weight.  For this formula to work, we will need additional statistics.  Since we are calculating for Saturn specifically, I took the values found from the NASA stats page linked earlier.

  • G = The Gravitational Constant (6.67*10^-11 N^2x m^2/kg^2)
  • m_1 = Object 1 Mass, Saturn (5.68*10^26 kg)
  • m_2 = Object 2 Mass, Person (45.5 kg)
  • r = Mean Radius, Saturn (5.82*10^7)

Now that we have all the variables needed, we can use Newton’s formula to get the result:

F_1 = (6.67*10^-11)\frac{(5.68*10^26)(45.5)}{(5.82*10^7)^2}

F_1 = \frac{1.72*10^18}{3.39*10^15}

F_1= 508N

Now we have the gravitational force (F) for Saturn.  In order to make a comparison based on weight, we will also need to do the same calculations for Earth.  Since we already have the gravitational constant and our calculated mass, we need to acquire Earth’s mean radius and it’s mass in kilograms.  These can both be found through the site linked earlier.

  • G = The Gravitational Constant (6.67*10^-11 N^2x m^2/kg^2)
  • m_1 = Object 1 Mass, Earth (5.97*10^24 kg)
  • m_2 = Object 2 Mass, Person (45.5 kg)
  • r = Mean Radius, Earth (6.37*10^6)

Once again we can use Newton’s formula to calculate the value of F:

F_2 = (6.67*10^-11)\frac{(5.97*10^24)(45.5)}{(6.37*10^6)^2}

F_2 = \frac{1.81*10^16}{4.06*10^13}

F_2= 446N

Now that we have both values we can compute the ratio:

R = \frac{F_1}{F_2} – where F_1 is the value of Saturn and F_2 is Earth.

R = \frac{508}{446}

R = 1.14

Curiously enough, the ratio arrived at in this equation is higher than the 1.065 cited in the NASA document.  I am assuming this is due to differences in the value used for each planet’s radius.  I will see what I can do about further investigating this discrepancy and amend my post if needed.

Now, to finish our process.  We once again cross-multiply using 100lbs to 1 for the value on Earth.

\frac{100 lbs.}{1} = \frac{x}{1.14}

100 * 1.14 = x * 1

x = 114 lbs

In conclusion, the variations in answer can be explained by taking into account the differences in radius values used in the calculations.  Polar radius, Equatorial radius and mean radius will all give values slightly different from one another in a difference of P_r < m_r < E_r.

With our calculations it can be assumed that we have a possibility for error.  Based on this information and given a discrepancy of a significant 7.4 lbs, this could account for roughly 7-13% variance in answers to this question.  That said, make certain to note which radius measurement is being asked for when calculating these types of problems.  It could mean the difference between a right and wrong answer.